五自由度机械臂的建模 (4) —— 四元数与空间旋转
四元数 (Quaternion) 是由爱尔兰数学家威廉·卢云·哈密顿在 1843 年提出的数学概念。从明确地角度而言,四元数是复数的不可交换延伸。相对于复数为二维空间,如果把四元数的集合考虑成多维实数空间,四元数就代表着一个四维空间。它可以用于描述现实空间的坐标。单位四元数 (Unit Quaternion) 可以用于表示三维空间中的旋转,它与常用的另外两种表示方式,即三维正交矩阵和欧拉角是等价的,但是避免了欧拉角表示法中的万向锁问题。
四元数
定义
复数是由实数加上虚数单位 \(i\) 组成,其中 \(i^{2} = -1\)。类似地,四元数是由实数加上三个元素 \(i\)、\(j\)、\(k\) 组成,且这三个元素满足
\[ i^{2} = j^{2} = k^{2} = ijk = -1 \]
每个四元数都是 \(1\)、\(i\)、\(j\)、\(k\) 的线性组合,即四元数一般可以表示为
\[ h = a + bi + cj + dk \]
为了便于说明和计算,这里也将四元数 \(h\) 表示为 \(h = (a, b, c, d)\)。
性质
乘法不可交换
\[ \begin{aligned} & ij = k, ji = -k \\ & jk = i, kj = -i \\ & ki = j, ik = -j \end{aligned} \]
共轭:四元数 \(h = a + bi + cj + dk\) 的共轭定义为
\[ h^{*} = a - bi - cj - dk \]
且一般情况下
\[ (hk)^{*} = k^{*} h^{*} = h^{*} k^{*} \]
模(绝对值)
\[ |h| = \sqrt{h \cdot h} =\sqrt{h \cdot h^{*}} = \sqrt{a^{2} + b^{2} + c^{2} + d^{2}} \]
乘逆 \[ h^{-1} = \frac{h^{*}}{|h|^{2}} \]
四元数运算
定义两个四元数
\[ \begin{aligned} q & = a + \vec{u} = a + bi + cj + dk \\ p & = t + \vec{v} = t + xj + yj + zk \end{aligned} \]
加法
\[ p + q = a + t + \vec{u} + \vec{v} = (a + t) + (b + x)j + (c + y)j + (d + z)k \]
加法遵循实数和复数的所有交换律和结合律。
乘法(格拉斯曼积)
\[ \begin{aligned} pq & = at - \vec{u} \cdot \vec{v} + a \vec{v} + t \vec{u} + \vec{u} \times \vec{v} \\ & = (at - bx - cy - dz) + (bt + ax + dy -cz)i + (ct + ay + bz - dx)j + (dt + za + cx - by)k \end{aligned} \]
点积(欧几里得内积):四元数的点积等同于一个四维矢量的点积,是一个标量 \[ p \cdot q = at + \vec{u} \cdot \vec{v} = at + bx + cy + dz \] 可以用格拉斯曼积表示为 \[ p \cdot q = \frac{pq + qp}{2} \]
单位四元数与空间旋转
单位四元数 (Unit Quaternion) 可以用于表示三维空间中的旋转,它与常用的另外两种表示方式,即三维正交矩阵和欧拉角是等价的,但是避免了欧拉角表示法中的万向锁问题。用四元数来表示旋转要解决两个问题:一是如何用四元数表示三维空间里的点;二是如何用四元数表示三维空间的旋转。
点的表示
对于三维空间中的一点 \(p\) 的笛卡尔坐标为 \((x, y, z)\),其可用纯四元数(即实部为 \(0\) 的四元数)表示为
\[ p = xj + yj + zk \]
旋转的表示
设 \(q\) 为一个单位四元数,\(p\) 是一个纯四元数(即空间中的一个点),定义纯四元数
\[ R_{q}(p) = q p q^{-1} \]
表示空间中的点 \(p\) 经过旋转 \(q\) 后得到的空间中的另一个点。
旋转的复合
根据四元数表示空间旋转的定义,有
\[ R_{q_{1} q_{2}} (p) = (q_{1} q_{2}) p (q_{1} q_{2})^{-1} = q_{1} q_{2} p q_{2}^{-1} q_{1}^{-1} = R_{q_{1}} \left[ R_{q_{2}} (p) \right] \]
因此,对于两个旋转的复合,只需要将对应的单位四元数相乘。
旋转矩阵与单位四元数
旋转矩阵、欧拉角和 RPY 角
旋转矩阵
空间中一点绕 \(x\)、\(y\)、\(z\) 轴旋转的旋转矩阵分别为
\[ \begin{aligned} & R_{x}(\theta_{1}) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\theta_{1}} & -\sin{\theta_{1}} \\ 0 & \sin{\theta_{1}} & \cos{\theta_{1}} \end{bmatrix} \\ & R_{y}(\theta_{2}) = \begin{bmatrix} \cos{\theta_{2}} & 0 & \sin{\theta_{2}} \\ 0 & 1 & 0 \\ -\sin{\theta_{2}} & 0 & \cos{\theta_{2}} \end{bmatrix} \\ & R_{z}(\theta_{3}) = \begin{bmatrix} \cos{\theta_{3}} & -\sin{\theta_{3}} & 0 \\ \sin{\theta_{3}} & \cos{\theta_{3}} & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]
其中,有三个独立变量 \(\theta_{1}\)、\(\theta_{2}\) 和 \(\theta_{3}\),通常有两种表示方式,即欧拉角和 RPY 角。
欧拉角
下图所示为常用的 ZXZ 顺规欧拉角的定义
设 \(xyz\) 轴为参考坐标系的坐标轴,\(xy\) 平面与 \(XY\) 平面的交线 \(N\) 称为交点线。则 ZXZ 顺规的欧拉角可以静态地定义为:
- \(\alpha\):\(x\) 轴与 \(N\) 的夹角
- \(\beta\):\(z\) 轴与 \(Z\) 轴的夹角
- \(\gamma\):\(N\) 与 \(X\) 轴的夹角
其旋转矩阵为
\[ \begin{aligned} R & = R_{z}(\alpha) R_{x}(\beta) R_{z}(\gamma) \\ & = \begin{bmatrix} \cos{\alpha} & -\sin{\alpha} & 0 \\ \sin{\alpha} & \cos{\alpha} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\beta} & -\sin{\beta} \\ 0 & \sin{\beta} & \cos{\beta} \end{bmatrix} \begin{bmatrix} \cos{\gamma} & -\sin{\gamma} & 0 \\ \sin{\gamma} & \cos{\gamma} & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{aligned} \]
ZXZ 顺规欧拉角的动态演示如下图所示
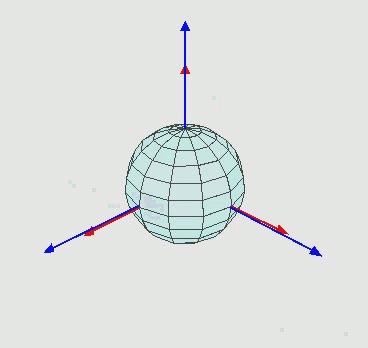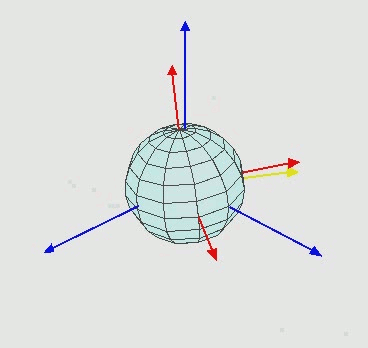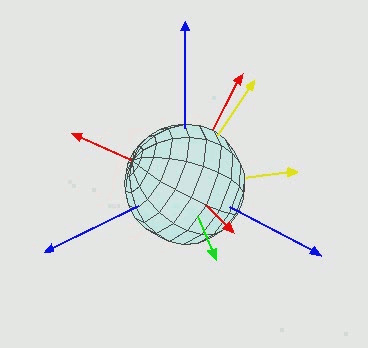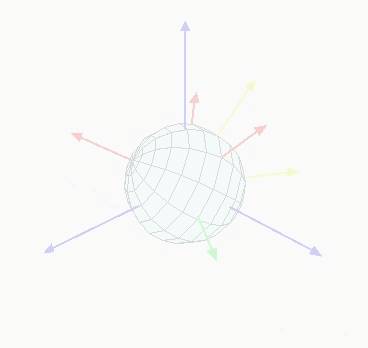
RPY 角
RPY 角即绕 \(X\) 轴摇摆 (Roll) \(\gamma\)、绕 \(Y\) 轴俯仰 (Pitch) \(\beta\)、绕 \(Z\) 轴偏转 (Yaw) \(\alpha\),这三个变量互相独立。RPY 角表示法与 ZYX 顺规的欧拉角表示方式等价,其旋转矩阵为
\[ \begin{aligned} R & = R_{z}(\alpha) R_{y}(\beta) R_{x}(\gamma) \\ & = \begin{bmatrix} \cos{\alpha} & -\sin{\alpha} & 0 \\ \sin{\alpha} & \cos{\alpha} & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos{\beta} & 0 & \sin{\beta} \\ 0 & 1 & 0 \\ -\sin{\beta} & 0 & \cos{\beta} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos{\gamma} & -\sin{\gamma} \\ 0 & \sin{\gamma} & \cos{\gamma} \end{bmatrix} \end{aligned} \]
旋转矩阵转换为四元数
已知旋转矩阵
\[ R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{12} & r_{13} \\ r_{31} & r_{12} & r_{13} \end{bmatrix} \]
其对应的四元数 \(q = w + xi + yj + zk\) 或 \(q = (w, x, y, z)\),其中
\[ \begin{aligned} w & = \frac{1}{2} \sqrt{1 + r_{11} + r_{22} + r_{33}} \\ x & = \frac{r_{32} - r_{23}}{4 w} \\ y & = \frac{r_{13} - r_{31}}{4 w} \\ z & = \frac{r_{21} - r_{12}}{4 w} \end{aligned} \]
故可得空间中一点绕 \(x\)、\(y\)、\(z\) 轴旋转的四元数表示为
\[ \begin{aligned} q_x(\theta_{1}) & = (\cos{\frac{\theta_{1}}{2}}, \sin{\frac{\theta_{1}}{2}}, 0, 0) \\ q_y(\theta_{2}) & = (\cos{\frac{\theta_{2}}{2}}, 0, \sin{\frac{\theta_{2}}{2}}, 0) \\ q_z(\theta_{3}) & = (\cos{\frac{\theta_{3}}{2}}, 0, 0, \sin{\frac{\theta_{3}}{2}}) \end{aligned} \]
四元数转换为旋转矩阵
对于四元数 \(q = (w, x, y, z)\),可以得到对应的旋转矩阵
\[ R = \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{12} & r_{13} \\ r_{31} & r_{12} & r_{13} \end{bmatrix} \]
其中,
\[ \begin{aligned} r_{11} & = w^{2} + x^{2} - y^{2} -z^{2} \\ r_{12} & = 2xy - 2wz \\ r_{13} & = 2xz + 2wy \\ r_{21} & = 2xy + 2wz \\ r_{22} & = w^{2} - x^{2} + y^{2} - z^{2} \\ r_{23} & = 2yz - 2wx \\ r_{31} & = 2xz - 2wy \\ r_{32} & = 2yz + 2wx \\ r_{33} & = w^{2} - x^{2} - y^{2} + z^{2} \end{aligned} \]
RPY 角转换为四元数
若旋转由 RPY 角(或 ZYX 顺规的欧拉角)表示,即绕参考坐标系的 \(Z\)、\(Y\) 和 \(X\) 轴依次旋转 \(\gamma\)、\(\beta\) 和 \(\alpha\) 角,则此旋转的四元数表示为 \(q = (w, x, y, z)\),其中
\[ \begin{aligned} w & = \cos{\frac{\alpha}{2}} \cos{\frac{\beta}{2}} \cos{\frac{\gamma}{2}} + \sin{\frac{\alpha}{2}} \sin{\frac{\beta}{2}} \sin{\frac{\gamma}{2}} \\ x & = \sin{\frac{\alpha}{2}} \cos{\frac{\beta}{2}} \cos{\frac{\gamma}{2}} - \cos{\frac{\alpha}{2}} \sin{\frac{\beta}{2}} \sin{\frac{\gamma}{2}} \\ y & = \cos{\frac{\alpha}{2}} \sin{\frac{\beta}{2}} \cos{\frac{\gamma}{2}} + \sin{\frac{\alpha}{2}} \cos{\frac{\beta}{2}} \sin{\frac{\gamma}{2}} \\ z & = \cos{\frac{\alpha}{2}} \cos{\frac{\beta}{2}} \sin{\frac{\gamma}{2}} + \sin{\frac{\alpha}{2}} \sin{\frac{\beta}{2}} \cos{\frac{\gamma}{2}} \\ \end{aligned} \]
四元数转换为 RPY 角
对于四元数 \(q = (w, x, y, z)\),可以得到对应的 RPY 角
\[ \begin{aligned} \theta_{R} & = \arctan{\left[ \frac{2(yz+wx)}{w^{2} - x^{2} - y^{2} + z^{2}} \right]} \\ \theta_{P} & = \arcsin{[-2(xz - wy)]} \\ \theta_{Y} & = \arctan{\left[ \frac{2(xy + wz)}{w^{2} + x^{2} - y^{2} - z^{2}} \right]} \end{aligned} \]